Tag Archives: solution agrees with answer key

How To Prove It by Velleman

Prove It by Velleman, Section 3.1, Problem 9

Leave a comment

Problem

Suppose a and b are real numbers. Prove that if a < b then \frac{a+b}{2} < b .

Solution

Given:

  • a and b are real
  • a < b

Goal:

  • \frac{a+b}{2} < b

a – b < 0. Add 2b on both sides to get a + b < 2b. Divide by 2.

Form:

Suppose a < b

— Proof of \frac{a+b}{2} < b goes here.

Therefore, if a < b then \frac{a+b}{2} < b .

Proof: Suppose a < b. Adding b to both sides we get a + b < 2b. Dividing by 2 we get \frac{a+b}{2} < b as required. Thus, if a < b, then \frac{a+b}{2} < b .

How To Prove It by Velleman

Prove It by Velleman, Section 3.1, Problem 1

Leave a comment

Problem

Consider the following theorem. (This theorem was proven in the introduction.)

1. Identify the hypotheses and conclusion of the theorem. Are the hypotheses true when n = 6? What does the theorem tell you in this instance? Is it right?

2. What can you conclude from the theorem in the case n = 15? Check directly that this conclusion is correct.

3. What can you conclude from the theorem in the case n = 11?

Solution

1. Identify the hypotheses and conclusion of the theorem. Are the hypotheses true when n = 6? What does the theorem tell you in this instance? Is it right?

The hypotheses are: n \in \mathcal{Z} , n > 1, and n is not prime.

The conclusion is 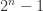2^n - 1 is not prime.

6 is an integer. 6 > 1. 6 is not prime. The hypotheses are true when n = 6.

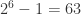2^6 - 1 = 63 , which is not prime, so this instance of the theorem is correct.

2. What can you conclude from the theorem in the case n = 15? Check directly that this conclusion is correct.

The hypotheses are true when n = 15.

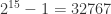2^{15} - 1 = 32767 which is not prime (32767 is divisible by 7). So this instance of the theorem is correct.

3. What can you conclude from the theorem in the case n = 11?

11 is not prime so the hypothesis, n is not prime, is false. Therefore, the theorem does not apply.

How To Prove It by Velleman

Prove It by Velleman, Section 2.3, Problem 13

Leave a comment

Problem

13. Sometimes each set in an indexed family of sets has *two* indices. For this problem, use the following definitions: I = {1,2}, J = {3,4}. For each i \in I and j \in J , let A _{i,j} = \{i, j, i+j\} . Thus, for example, A _{2,3} = \{2, 3, 5 \} .

1. For each j \in J let B_j = \bigcup \limits_{i \in I} A_{i,j} = A_{1,j} \cup A_{2,j} . Find B_3 and B_4 .
2. Find \bigcap \limits{j \in J} B_j . (Note that, replacing B_j with its definition, we could say that \bigcap \limits_{j \in J} B_j = \bigcap \limits_{j \in J} (\bigcup \limits_{i \in I} A_{i,j}) .)
3. Find \bigcup \limits_{i \in I} (\bigcap \limits_{j \in J} A_{i,j}) . (Hint: You may want to do this in two steps, corresponding to parts 1 and 2.) Are \bigcap \limits_{j \in J} (\bigcup \limits_{i \in I} A_{i,j}) and \bigcup \limits_{i \in I} ( \bigcap \limits_{j \in J} A_{i,j}) equal?
4. Analyze the logical forms of the statements x \in \bigcap \limits_{j \in J} (\bigcup \limits_{i \in I} A_{i,j}) and x \in \bigcup \limits_{i \in I} (\bigcap \limits_{j \in J} A_{i,j}) . Are they equivalent?

Solution

1. For each j \in J let B_j = \bigcup \limits_{i \in I} A_{i,j} = A_{1,j} \cup A_{2,j} . Find B_3 and B_4 .

A_{1,3} = \{1, 3, 4\}

A_{1,4} = \{1, 4, 5\}

A_{2,3} = \{2, 3, 5\}

A_{2,4} = \{2, 4, 6\}

B_3 = { 1, 2, 3, 4, 5 }

B_4 = { 1, 2, 4, 5, 6 }

2. Find \bigcap \limits{j \in J} B_j . (Note that, replacing B_j with its definition, we could say that \bigcap \limits_{j \in J} B_j = \bigcap \limits_{j \in J} (\bigcup \limits_{i \in I} A_{i,j}) .)

\bigcap \limits{j \in J} B_j = { 1, 2, 4, 5 }

3. Find \bigcup \limits_{i \in I} (\bigcap \limits_{j \in J} A_{i,j}) . (Hint: You may want to do this in two steps, corresponding to parts 1 and 2.) Are \bigcap \limits_{j \in J} (\bigcup \limits_{i \in I} A_{i,j}) and \bigcup \limits_{i \in I} ( \bigcap \limits_{j \in J} A_{i,j}) equal?

Let C_i = \bigcap \limits_{j \in J} A_{i,j}

C_1 = { 1, 4 }

C_2 = { 2 }

\cup i \in I C_i = { 1, 2, 4 }

{ 1, 2, 4 } \neq { 1, 2, 4, 5 }

\bigcap \limits_{j \in J} (\bigcup \limits_{i \in I} A_{i,j}) and \bigcup \limits_{i \in I} ( \bigcap \limits_{j \in J} A_{i,j}) are not equal.

4. Analyze the logical forms of the statements x \in \bigcap \limits_{j \in J} (\bigcup \limits_{i \in I} A_{i,j}) and x \in \bigcup \limits_{i \in I} (\bigcap \limits_{j \in J} A_{i,j}) . Are they equivalent?

x \in \bigcap \limits_{j \in J} (\bigcup \limits_{i \in I} A_{i,j}) = \forall x \forall j \in J \exists i \in I x \in A_{i,j}

x \in \bigcup \limits_{i \in I} (\bigcap \limits_{j \in J} A_{i,j}) = \forall x \exists i \in I \forall j \in J x \in A_{i,j}

We see that \forall j \in J and \exists i \in I are swapped. The existential and universal quantifiers are not commutative with each other. So the statements are not equivalent.

How To Prove It by Velleman

Prove It by Velleman, Section 2.3, Problem 8

Leave a comment

Problem

Let I = {2, 3}, and for each i \in I let A_i = {i, 2i} and B_i = {i, i+1} .

1. List the elements of the set A_i and B_i for i \in I .
2. Find \bigcap \limits_{i \in I} (A_i \cup B_i) and (\bigcap \limits_{i \in I} A_i) \cup (\bigcap \limits_{i \in I} B_i) . Are they the same?
3. In parts 3 and 4 of exercise 2 you analyzed the statements x \in \bigcap \limits_{i \in I} (A_i \cup B_i) and  x \in (\bigcap \limits_{i \in I} A_i) \cup (\bigcap \limits_{i \in I} B_i) . What can you conclude from your answer to part 2 about whether or not these statements are equivalent?

Solution

1. List the elements of the set A_i and B_i for i \in I .

A_2 = {2, 4}

A_3 = {3, 6}

B_2 = {2, 3}

B_3 = {3, 4}

2. Find \bigcap \limits_{i \in I} (A_i \cup B_i) and (\bigcap \limits_{i \in I} A_i) \cup (\bigcap \limits_{i \in I} B_i) . Are they the same?

A_2 \cup B_2 = {2, 3, 4}

A_3 \cup B_3 = {3, 4, 6}

\bigcap \limits_{i \in I} (A_i \cup B_i) = {3, 4}

\bigcap \limits_{i \in I} A_i = \emptyset

\bigcap \limits_{i \in I} B_i = {3}

(\bigcap \limits_{i \in I} A_i) \cup (\bigcap \limits_{i \in I} B_i) = {3}

3. In parts 3 and 4 of exercise 2 you analyzed the statements x \in \bigcap \limits_{i \in I} (A_i \cup B_i) and  x \in (\bigcap \limits_{i \in I} A_i) \cup (\bigcap \limits_{i \in I} B_i) . What can you conclude from your answer to part 2 about whether or not these statements are equivalent?

They are not equivalent. This confirms that the universal quantifier does not distribute over disjunction.

How To Prove It by Velleman

Prove It by Velleman, Section 2.3, Problem 1

Leave a comment

Problem

Analyze the logical forms of the following statements. You may use the symbols \in, \notin, =, \neq, \land, \lor, \to, \iff, \forall, \text{and } \exists in your answers, but not \subseteq, \subsetneq, \mathcal P, \cap, \cup, \setminus, \{, \}, \text{or } \neg . (Thus, you must write out the definitions of some set theory notation, and you must use equivalences to get rid of any occurrences of \neg .)

  1. \mathcal F \subseteq \mathcal P (A)
  2. A \subseteq \{2n + 1 \mid n \in \mathbb{N}\}
  3. \{n^2 + n + 1 \mid n \in \mathbb{N} \} \subseteq \{2n + 1 \mid n \in \mathbb{N} \}
  4. \mathcal P (\bigcup \limits _{i \in I} A_i) \subsetneq \bigcup \limits _{i \in I} \mathcal P (A_i)

 

Solution

1.

\mathcal F \subseteq \mathcal P (A)

\mathcal F is a family of sets. Any member of \mathcal F , a set, is a power set of A.

So \text{every member of } \mathcal F \subseteq A .

Every member of \mathcal F is in $latex  \mathcal P(A) $

\forall y (y \in F \to y \in \mathcal P(A))

To say that y \in \mathcal P (A) means that y \subseteq A .

\forall y (y \in F \to y \subseteq A)

We’ll introduce x to mean a member of y.

\forall y (y \in F \to \forall x ( x \in y \to x \in A))

2.

A \subseteq \{2n + 1 \mid n \in \mathbb{N}\}

Definition of subset:

A \subseteq B = \forall x (x \in A \to x \in B)

\forall x ( x \in A \to \exists n \mathbb{N} (x = 2n + 1))

3.

\{n^2 + n + 1 \mid n \in \mathbb{N} \} \subseteq \{2n + 1 \mid n \in \mathbb{N} \}

Definition of subset:

A \subseteq B = \forall x (x \in A \to x \in B)
\forall n \in \mathbb{N} \exists m \in \mathbb{N} (n^2 + n + 1 = 2m + 1)

Need to use n and m to allow for different values, since these were two different statements.

4.

\mathcal P (\bigcup \limits _{i \in I} A_i) \subsetneq \bigcup \limits _{i \in I} \mathcal P (A_i)

There is some set that is a power set of the union of the family of A that is not a subset of the union of all power sets of the family of A.

\mathcal P (\bigcup \limits _{i \in I} A_i) \subsetneq \bigcup \limits _{i \in I} \mathcal P (A_i)

Add some context

\exists y [ y \in \mathcal{P} (\bigcup \limits_{i \in I} A_i) \land y \notin \bigcup \limits_{i \in I} \mathcal P(A_i)]

Power Set: y \in \mathcal{P} (\bigcup \limits_{i \in I} A_i) = \forall x (x \in y \to x \in \bigcup \limits_{i \in I} A_i) .

\exists y [ \forall x (x \in y \to x \in \bigcup \limits_{i \in I} A_i) \land y \notin \bigcup \limits_{i \in I} \mathcal{P}(A_i)]

Family Union: x \in \bigcup \limits_{i \in I} A_i = \exists i \in I (x \in A_i)

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land y \notin \bigcup \limits_{i \in I} \mathcal{P}(A_i)]

Negation

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land \neg (y \in \bigcup \limits_{i \in I} \mathcal P(A_i))]

Does this work? What does it mean to be a union of power sets? Same goes for the question itself.

Family Union: y \in \bigcup \limits_{i \in I} \mathcal P(A_i) = \exists i \in I \forall x (x \in y \to x \in \mathcal P(A_i) . If y contains all the members x, then there is a set A_i that also contains all members x.

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land \neg (\exists i \in I \forall x (x \in y \to x \in \mathcal P(A_i)))]

Power Set: x \in \mathcal P(A_i) = x \in y \to x \in A_i

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land \neg (\exists i \in I \forall x (x \in y \to (x \in y \to x \in A_i)))]

Conditional

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land \neg (\exists i \in I \forall x (x \notin y \lor x \notin y \lor x \in A_i)))]

Tautology

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land \neg (\exists i \in I \forall x (x \notin y \lor x \in A_i)))]

Quantifier Negation and DeMorgan

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land (\forall i \in I \exists x (x \in y \land x \notin A_i)))]

How To Prove It by Velleman

Prove It by Velleman, Section 2.2, Problem 6

Leave a comment

Problem

Show that existential quantifier distributes over disjunction. In other words, show that \exists x (P(x) \lor Q(x)) is equivalent to \exists x P(x) \lor \exists x Q(x) . (Hint: Use the fact, discussed in this section, that the universal quantifier distributes over conjunction.)

 

Solution

We know that, universal quantifier distribute over conjunction so:

\forall x [\neg P(x) \land \neg Q(x)] = [\forall x \neg P(x)] \land [\forall x \neg Q(x)]

Negate both sides

\neg \forall x [\neg P(x) \land \neg Q(x)] = \neg ( [\forall x \neg P(x)] \land [\forall x \neg Q(x)] )

Quantifier Negate

\exists x \neg [\neg P(x) \land \neg Q(x)] = \neg ( [\forall x \neg P(x)] \land [\forall x \neg Q(x)] )

DeMorgan

\exists x [P(x) \lor Q(x)] = ( \neg [\forall x \neg P(x)] \lor \neg [\forall x \neg Q(x)] )

Quanitifer Negate and Double Negation

\exists x [P(x) \lor Q(x)] = \exists x P(x) \lor \exists x Q(x)] )