Problem
- Prove that if
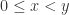 , then
, then 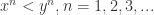
- Prove that if
 and n is odd, then
and n is odd, then  .
.
- Prove that if
 and n is odd, then
and n is odd, then 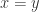 .
.
- Prove that if
 and n is even, then
and n is even, then 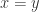 or
or 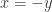 .
.
Solution
Prove that if 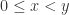 , then
, then 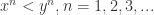
In Problem 5 we showed that if  and
and 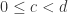 , then
, then 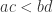 . Let
. Let  and
and 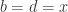 , which implies
, which implies 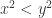 .
.
Now consider if  ,
,  ,
,  , and
, and  . By the same logic, we see that
. By the same logic, we see that  . Now, we can repeat the process again by setting
. Now, we can repeat the process again by setting  and
and  . In fact, we can do this again and again ad infinitum.
. In fact, we can do this again and again ad infinitum.
Therefore, if if 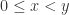 and
and 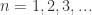 , then , then
, then , then  .
.
Prove that if  and n is odd, then
and n is odd, then  .
.
Consider the case where 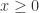 . This is the same as the previous part.
. This is the same as the previous part.
Consider the case where  . From the text we learn that when
. From the text we learn that when 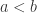 ,
,  is positive. If we apply this to
is positive. If we apply this to 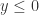 , we see that
, we see that 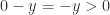 . We also see that
. We also see that 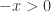 and
and 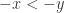 . Using what we proved in the previous part, we know that
. Using what we proved in the previous part, we know that 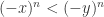 .
.
By closure under multiplication  . Let
. Let 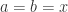 , so
, so 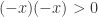 . In fact, any pair,
. In fact, any pair, 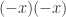 ,
, 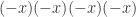 ,
,  , …, will always be positive. So we know that
, …, will always be positive. So we know that  . Similarly, we know that
. Similarly, we know that  . By extension,
. By extension, 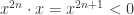 . So for any odd exponent
. So for any odd exponent 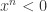 . Where n is odd, we do not change signs. So we know that
. Where n is odd, we do not change signs. So we know that 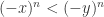 where n is odd.
where n is odd.
Finally, we have the case where 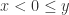 . We have shown earlier that where n is odd,
. We have shown earlier that where n is odd, 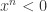 . On the other hand,
. On the other hand,  . So again
. So again  .
.
Prove that if  and n is odd, then
and n is odd, then 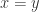 .
.
Assume  . So either
. So either  or
or 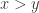 .
.
If  , by part 2 above, we know that it must be that
, by part 2 above, we know that it must be that  , since n is odd. This contradicts our given that
, since n is odd. This contradicts our given that  .
.
If 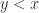 , by part 2 above, we know that it must be that
, by part 2 above, we know that it must be that 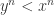 , since n is odd. This contradicts our given that
, since n is odd. This contradicts our given that  .
.
Since our assumption leads to contradictions, it must be that when  and n is odd that
and n is odd that 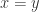 .
.
Prove that if  and n is even, then
and n is even, then 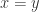 or
or 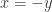 .
.
Consider the case where  . Assume
. Assume  . Applying the proof in part 1, if
. Applying the proof in part 1, if 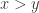 then
then  . Similarly, if
. Similarly, if 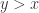 then
then 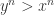 . In either case, we contradict our given that
. In either case, we contradict our given that  . Therefore, it must be that
. Therefore, it must be that 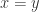 .
.
Consider the case where 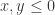 . Assume
. Assume  . In this case
. In this case 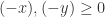 . Applying the proof in part 1, if
. Applying the proof in part 1, if 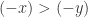 then
then 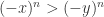 . Similarly, if
. Similarly, if 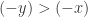 then
then 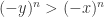 . In either case, we contradict our given that
. In either case, we contradict our given that  . Therefore, it must be that
. Therefore, it must be that 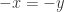 .
.
Finally, consider the case where 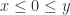 . Assume
. Assume  . In this case
. In this case 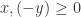 . Applying the proof in part 1, if
. Applying the proof in part 1, if  then
then 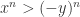 . Similarly, if
. Similarly, if  then
then 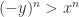 . In either case, we contradict our given that
. In either case, we contradict our given that  . Therefore, it must be that
. Therefore, it must be that 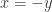 .
.
Therefore, if  and n is even, then
and n is even, then 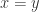 or
or 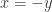 .
.
for which
.
.
.
.
. This is nonsense.
. This is nonsense.
or
.
. Nonsense.
. No use here.
. However, try letting
. You get
. Doesn’t work.
, the distance from
to
must be 2. So there is no number in
that satisfies this inequality.
to
must be 2, it certainly cannot be less than 1.
or
. The absolute value doesn’t even matter in this problem. So
or
.
or
. In this case
. Expand to get
. Using the quadratic formula
.
and
so that fits what we’re looking for.
, we know that
. The solution here is
, which is not
.