Tag Archives: no answer key

How To Prove It by Velleman

Prove It by Velleman, Section 3.1, Problem 10

Leave a comment

Problem

Suppose x is a real number and x \neq 0 . Prove that if \frac{\sqrt[x]{x} + 5}{x+6} = \frac{1}{x} then x \neq 8 .

Solution

Given:

  • x is real
  • x \neq 0
  • \frac{\sqrt[x]{x} + 5}{x+6} = \frac{1}{x}

Goal:

  • x \neq 8

\frac{\sqrt[x]{x} + 5}{x+6} = \frac{1}{x}

x^{4/3} + 5x = x + 6

x^{4/3} + 4x = 6

If x were 8, then the left side would be 48.

It might be easier to prove the contrapositive.

Form:

Supppose x \neq 8 is false.

— Proof that \frac{\sqrt[x]{x} + 5}{x+6} \neq \frac{1}{x} goes here.

Therefore, if \frac{\sqrt[x]{x} + 5}{x+6} = \frac{1}{x} then x \neq 8 .

Proof: We will prove the contrapositive. Multiplying both sides by (x + 6) and x, we get x^{4/3} + 4x \neq 6 . If x = 8, we conclude that 48 \neq 6 . Thus, if \frac{\sqrt[x]{x} + 5}{x+6} = \frac{1}{x} then x \neq 8 .

How To Prove It by Velleman

Prove It by Velleman, Section 3.1, Problem 8

Leave a comment

Problem

Suppose A \setminus B \subseteq C \cap D and x \in A . Prove that if x \notin D then x \in B .

Solution

Given:

  • A \setminus B \subseteq C \cap D
  • x \in A
  • x \notin D

Goal:

  • x \in B

So the logic version is \forall x (x \in A \land x \notin B \to x \in C \land x \in D) . Since x \notin D , the right side is false. This is a conditional statement, so the only way the statement can be true is if the left side is also false. Since x \in A the only way to make the left side false is if x \in B .

Form:

Suppose x \notin D

— Proof of x \in B goes here.

Therefore, if x \notin D , then x \in B .

Proof: Suppose A \setminus B \subseteq C \cap D , x \in A , and x \notin D . We conclude that x \notin C \cap D . Similarly x \notin A \setminus B . However, we know that x \in A , so we conclude that x \in B , as required. Therefore if x \notin D then x \in B .

How To Prove It by Velleman

Prove It by Velleman, Section 3.1, Problem 7

Leave a comment

Problem

Suppose that a is a real number. Prove that if a^3 > a then a^5 > a . (Hint: One approach is to start by completing the following equation: a^5 - a = (a^3 - a) \cdot ? .)

Solution

 Given:

  • a is real
  • a^3 > a

 Goal:

  • a^5 > a

The tactic is to figure out the ratio between a^3 and a^5 .

a^5 - a = (a^3 - a) \cdot x

x = \frac{a^5 -a}{a^3 - a}

Factor

x = \frac{(a^2 + 1) (a^2 - 1)}{a^2 - 1}

x = a^2 + 1

We know that a^2 is a positive number, so a^2 + 1 is a positive number greater than 1.

So we know the multiplier to from from a^3 - a to a^5 - a is a positive number greater than 1.

Form:

Suppose a^3 > a .

— Proof of a^5 > a goes here.

Therefore, if a^3 > a , then a^5 > a .

Proof: Suppose a^3 > a . Subtracting a from both sides yields a^3 - a = 0 . Multiply both sides by (a^2 + 1) we get (a^3 - a) \cdot (a^2 + 1) = a^5 - a > 0 . Adding a to both sides, we get a^5 > a as required. Thus if a^3 > a then a^5 > a .

How To Prove It by Velleman

Prove It by Velleman, Section 3.1, Problem 6

Leave a comment

Problem

Suppose a and b are real numbers. Prove that if 0 < a < b then \frac{1}{b} < \frac{1}{a} .

Solution

Given:

  • a and b are real
  • 0 < a < b

Goal:

  • \frac{1}{b} < \frac{1}{a}

We know that a and b are positive, no sign change. We can divide by \frac{1}{ab}.

Form:

Suppose 0 < a < b

— Proof of \frac{1}{b} < \frac{1}{a} goes here.

Therefore, if 0 < a < b, then \frac{1}{b} < \frac{1}{a} .

 Proof: Suppose 0 < a < b, Multiplying the inequality a < b by the positive number \frac{1}{ab} we get \frac{1}{b} < \frac{1}{a} as required. Thus if 0 < a < b, then \frac{1}{b} < \frac{1}{a} .

How To Prove It by Velleman

Prove It by Velleman, Section 3.1, Problem 5

Leave a comment

Problem

Suppose a and b are real numbers. Prove that if a < b < 0 then a^2 > b^2 .

Solution

 Scratch:

 Given:

  • a and b are real
  • – a < b < 0

Goal:

  • a^2 > b^2

We know that a and b are negative, so multiplying would flip the sign.

 Form:

Suppose a < b < 0

— Proof of a^2 > b^2 goes here

Therefore, if a < b < 0, then a^2 > b^2 .

Proof: Suppose a < b < 0. Multiplying the inequality a < b by the negative number a we can conclude a^2 > ab and similarly multiplying by the negative number b we get ab > b^2 . Therefore a^2 > ab > b^2 , so a^2 > b^2 , as required. Thus if a < b < 0, then a^2 > b^2 .

How To Prove It by Velleman

Prove It by Velleman, Section 3.1, Problem 3

Leave a comment

Problem

Consider the following incorrect theorem:

Incorrect Theorem. Suppose n is a natural number larger than 2, and n is not a prime number. Then 2n + 13 is not a prime number.

What are the hypotheses and conclusion of this theorem? Show that the theorem is incorrect by finding a counterexample.

Solution

Hypotheses: n \in \mathcal{N} , n > 2, and n is not prime.

Conclusion: 2n + 13 is not prime.

n = 3

2 \cdot 3 + 13 = 19

19 is prime, so the theorem is false.

How To Prove It by Velleman

Prove It by Velleman, Section 3.1, Problem 2

Leave a comment

Problem

Consider the following theorem. (The theorem is correct, but we will not ask you to prove it here.)

Theorem. Suppose that 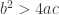b^2 > 4ac . Then the quadratic equation 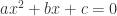ax^2 + bx + c = 0 has two real solutions.

1. Identify the hypotheses and conclusion of the theorem.
2. To give an instance of the theorem, you must specify values for a, b, and c, but not x. Why?
3. What can you conclude from the theorem in the case a = 2, b = -5, c = 3? Check directly that this conclusion is correct.
4. What can you conclude from the theorem in the case a = 2, b = 4, c = 3?

Solution

1. Identify the hypotheses and conclusion of the theorem.

Hypothesis: 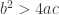b^2 > 4ac

Conclusion: 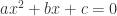ax^2 + bx + c = 0 has two real solutions

2. To give an instance of the theorem, you must specify values for a, b, and c, but not x. Why?

The general solution for a quadratic formula is 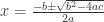x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} . The question concerns us with real versus imaginary solutions for x. That is determined solely by the term \sqrt{b^2-4ac}. If there were two real solutions, \sqrt{b^2-4ac} would be positive, or 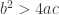b^2 > 4ac so it is sufficient to consider a, b, and c, but not x.

3. What can you conclude from the theorem in the case a = 2, b = -5, c = 3? Check directly that this conclusion is correct.

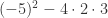
(-5)^2 - 4 \cdot 2 \cdot 3

25 - 24

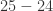
This is positive so we can conlude that there are two real solutions.

4. What can you conclude from the theorem in the case a = 2, b = 4, c = 3?

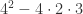
4^2 - 4 \cdot 2 \cdot 3

16 - 24

This is negative so we can conclude there wouldn’t be two real solutions.

How To Prove It by Velleman

Prove It by Velleman, Section 2.3, Problem 15

Leave a comment

Problem

In Section 2.3 we saw that a set can have other sets as elements. When discussing sets whose elements are sets, it might seem most natural to consider the universe of discourse to be collection of all sets. However, as we will see in this problem, assuming that there is such a universe leads to contradictions.

Suppose U were the collection of all sets. Note that in particular U is a set, so we would have U \in U . This is not yet a contradiction; although most sets are not elements of themselves, perhaps some sets are elements of themselves. But it suggests that the sets in the universe U could be split into two categories: the unusual sets that, like U itself, are elements of themselves, and the more typical sets that are not. Let R be the set of sets in the second category. In other words, R = \{ A \in U \mid A \notin A \} . This means that for any set A in the universe U, A will be an element of R iff A \notin A . In other words, we have \forall A \in U (A \in R \iff A \notin A) .

1. Show that applying this last fact to the set R itself (in other words, plugging in R for A) leads to a contradiction. This contradiction was discovered by Bertrand Russell in 1901, and is known as Russell’s Paradox.

2. Think some more about the paradox in part 1. What do you think it tells us about sets?

Solution

1. Show that applying this last fact to the set R itself (in other words, plugging in R for A) leads to a contradiction. This contradiction was discovered by Bertrand Russell in 1901, and is known as *Russell’s Paradox*.

\forall R \in U (R \in R \iff R \notin R)

Biconditional

\forall R \in U [(R \in R \to R \notin R) \land (R \notin R \to R \in R)]

Conditional

\forall R \in U [(R \notin R \lor R \notin R) \land (R \in R \lor R \in R)]

Idempotent

\forall R \in U (R \notin R \land R \in R)

This is a contradiction.

2. Think some more about the paradox in part 1. What do you think it tells us about sets?

It’s best to define sets to avoid recursive definitions.

How To Prove It by Velleman

Prove It by Velleman, Section 2.3, Problem 14

1 Comment

Problem

1. Show that if \mathcal F = \emptyset , then the statement x \in \cup \mathcal F will be false no matter what x is. It follows that \cup \emptyset = \emptyset .
2. Show that if \mathcal F = \emptyset , then the statement x \in \cap \mathcal F will be true to no matter what x is. In a context in which it is clear what the universe of discourse U is, we might therefore want to say that \cap \emptyset = U . However, this has the unfortunate consequence that the notation \cap \emptyset will mean different things in different contexts. Furthermore, when working with sets whose elements are sets, mathematicians often do not use a universe of discourse at all. (For more on this, see the next exercise.) For these reasons, some mathematicians consider the notation \cap \emptyset to be meaningless. We will avoid this problem in this book by using the notation \cap \mathcal F only in contexts in which we can be sure that \mathcal \neq \emptyset .

Soultion

1. Show that if \mathcal F = \emptyset , then the statement x \in \cup \mathcal F will be false no matter what x is. It follows that \cup \emptyset = \emptyset .

\cup \mathcal F = \forall A (A \in \mathcal F \land x \in A)

Substitute \emptyset for \mathcal F .

\cup \emptyset = \forall A (A \in \emptyset \land x \in A)

\emptyset by definition cannot contain anything. So we know that A \in \emptyset is always false. Since A \in \emptyset is the lead of a conjunction, we know that the entire statement is always false.

2. Show that if \mathcal F = \emptyset , then the statement x \in \cap \mathcal F will be true to no matter what x is. In a context in which it is clear what the universe of discourse U is, we might therefore want to say that \cap \emptyset = U . However, this has the unfortunate consequence that the notation \cap \emptyset will mean different things in different contexts. Furthermore, when working with sets whose elements are sets, mathematicians often do not use a universe of discourse at all. (For more on this, see the next exercise.) For these reasons, some mathematicians consider the notation \cap \emptyset to be meaningless. We will avoid this problem in this book by using the notation \cap \mathcal F only in contexts in which we can be sure that \mathcal \neq \emptyset .

\cap \mathcal F = \forall A (A \in \mathcal F \to x \in A)

Substitute \emptyset for \mathcal F .

\cap \emptyset = \forall A (A \in \emptyset \to x \in A)

\emptyset by definition cannot contain anything. So we know that A \in \emptyset is always false. Since A \in \emptyset is the lead of a conditional and always false, we know that the entire statement is always true, albeit vacuously.

How To Prove It by Velleman

Prove It by Velleman, Section 2.3, Problem 12

Leave a comment

Problem

Verify the following identities by writing out (using logical symbols) what it means for an object x to be an element of each set and then using logical equivalences.

1. \bigcup \limits_{i \in I} (A_i \cup B_i) = (\bigcup \limits_{i \in I} A_i) \cup (\bigcup \limits_{i \in I} B_i)
2. (\cap \mathcal F) \cap (\cap \mathcal G) = \cap (\mathcal F \cup \mathcal G)
3. \bigcap \limits_{i \in I} (A_i \setminus B_i) = (\bigcap \limits_{i \in I} A_i) \setminus (\bigcap \limits_{i \in I} B_i)

Solution

1. \bigcup \limits_{i \in I} (A_i \cup B_i) = (\bigcup \limits_{i \in I} A_i) \cup (\bigcup \limits_{i \in I} B_i)

General definition

x \in \bigcup \limits_{i \in I} A_i = \forall x \exists i \in I(x \in A_i)

So

\forall x \exists i \in I(x \in A_i \lor x \in B_i) = \forall x (\exists i \in I(x \in A_i) \lor \exists i \in I(x \in B_i))

Quantifier Distribution

\forall x \exists i \in I(x \in A_i \lor x \in B_i) = \forall x \exists i \in I(x \in A_i \lor x \in B_i)

2. (\cap \mathcal F) \cap (\cap \mathcal G) = \cap (\mathcal F \cup \mathcal G)

General Definition

x \in \cap \mathcal F = \forall A (A \in \mathcal F \to x \in A)

So

\forall A [(A \in \mathcal F \to x \in A) \land (A \in \mathcal G \to x \in A)] = \forall A [A \in (\mathcal F \cup \mathcal G) \to x \in A]

Conditional

\forall A [(A \notin \mathcal F \lor x \in A) \land (A \notin \mathcal G \lor x \in A)] = \forall A [A \in (\mathcal F \cup \mathcal G) \to x \in A]

Distributive

\forall A [(A \notin \mathcal F \land A \notin \mathcal G) \lor x \in A] = \forall A [A \in (\mathcal F \cup \mathcal G) \to x \in A]

DeMorgan

\forall A [\neg (A \in \mathcal F \lor A \in \mathcal G) \lor x \in A] = \forall A [A \in (\mathcal F \cup \mathcal G) \to x \in A]

Conditional

\forall A [(A \in \mathcal F \lor A \in \mathcal G) \to x \in A] = \forall A [A \in (\mathcal F \cup \mathcal G) \to x \in A]

Definition of Union

\forall A [A \in (\mathcal F \cup \mathcal G) \to x \in A] = \forall A [A \in (\mathcal F \cup \mathcal G) \to x \in A]

3. \bigcap \limits_{i \in I} (A_i \setminus B_i) = (\bigcap \limits_{i \in I} A_i) \setminus (\bigcap \limits_{i \in I} B_i)

General definition

\bigcap \limits_{i \in I} A_i = \forall x \forall i \in I(x \in A_i)

So

\forall x \forall i \in I(x \in A_i \land x \notin B_i) = \forall x \forall i \in I [(x \in A_i) \land \neg (x \in B_i)]

 On the right hand side, does it make sense to place \forall i \in I on the outside?

\forall x \forall i \in I(x \in A_i \land x \notin B_i) = \forall x \forall i \in I(x \in A_i \land x \notin B_i)