Tag Archives: sets

How To Prove It by Velleman

Prove It by Velleman, Section 2.3, Problem 6

Leave a comment

Problem

Let I = {2, 3, 4, 5}, and for each i \in I let A_i = {i, i+1, i-1, 2i\\} .

1. List the elements of all the sets A_i , for i \in I .

2. Find \bigcap \limits_{i \in I} A_i and \bigcup \limits_{i \in I} A_i .

Solution
1. List the elements of all the sets A_i , for i \in I .

A_2 = {2, 3, 1, 4}.

A_3 = {3, 4, 2, 6}.

A_4 = {4, 5, 3, 8}.

A_5 = {5, 6, 4, 10}.

2. Find \bigcap \limits_{i \in I} A_i and \bigcup \limits_{i \in I} A_i .

\bigcap \limits_{i \in I} A_i = {4}.

\bigcup \limits_{i \in I} A_i = {1, 2, 3, 4, 5, 6, 8, 10}.

How To Prove It by Velleman

Prove It by Velleman, Section 2.3, Problem 2

Leave a comment

Problem

Analyze the logical forms of the following statements. You may use the symbols \in, \notin, =, \neq, \land, \lor, \to, \iff, \forall, \text{and } \exists in your answers, but not \subseteq, \subsetneq, \mathcal{P}, \cap, \cup, \setminus, \{, \}, \text{or } \neg . (Thus, you must write out the definitions of some set theory notation, and you must use equivalences to get rid of any occurrences of \neg .)

  1. x \in \cup \mathcal{F} \setminus \cup \mathcal{G}
  2. \{x \in B \mid x \notin C \} \in \mathcal{P}(A)
  3. x \in \bigcap \limits_{i \in I} (A_i \cup B_i)
  4. x \in (\bigcap \limits_{i \in I} A_i) \cup (\bigcap \limits_{i \in I} B_i)

 

 

 

Solution

1.

x \in \cup \mathcal{F} \setminus \cup \mathcal{G}

x is a member of the union of the \mathcal{F} family but not in the union of the \mathcal{G} family.

x \in \cup \mathcal{F} = \forall x (\exists A \in \mathcal{F}(x \in A)

x \in \cup \mathcal{G} = \forall x (\exists B \in \mathcal{G}(x \in B)

Combine

\forall x[(\exists A \in \mathcal{F}(x \in A)) \land \neg (\exists B \in \mathcal{G}(x \in B)]

Abbreviation

\forall x[(\exists A (A \in \mathcal{F} \to x \in A)) \land \neg (\exists B (B \in \mathcal{G} \to x \in B)]

Quantifier Negation

\forall x[(\exists A (A \in \mathcal{F} \to x \in A)) \land (\forall B \neg (B \in \mathcal{G} \to x \in B)]

Conditional

\forall x[(\exists A (A \in \mathcal{F} \to x \in A)) \land (\forall B \neg (B \notin \mathcal{G} \lor x \in B)]

DeMorgan

\forall x[(\exists A (A \in \mathcal{F} \to x \in A)) \land (\forall B (B \in \mathcal{G} \land x \notin B)]

2.

\{x \in B \mid x \notin C \} \in \mathcal{P}(A)

x is a member of B and not a member of C. B and C are both power sets of A.

Is this right?

\{x \in B \mid x \notin C \} = \forall x (x \in B \land x \notin C)

y \in \mathcal{P}(A) = \forall x (x \in y \to x \in A)

Combine

\forall x [(x \in B \land x \notin C) \to x \in A]

 

3.

x \in \bigcap \limits_{i \in I} (A_i \cup B_i)

Family Intersection

x \in \bigcap \limits_{i \in I} C_i = \forall i \in I \forall x (x \in C_i)

Union

x \in A \bigcup B = x \in A \lor x \in B

Combine

\forall i \in I \forall x (x \in A_i \lor x \in B_i))

4.

x \in (\bigcap \limits_{i \in I} A_i) \cup (\bigcap \limits_{i \in I} B_i)

\forall x [\forall i \in I (x \in A_i) \lor \forall i \in I (x \in A_i)]

Cannot pull out \forall i \in I because universal quantifier does not distribute over disjunction.

How To Prove It by Velleman

Prove It by Velleman, Section 2.3, Problem 1

Leave a comment

Problem

Analyze the logical forms of the following statements. You may use the symbols \in, \notin, =, \neq, \land, \lor, \to, \iff, \forall, \text{and } \exists in your answers, but not \subseteq, \subsetneq, \mathcal P, \cap, \cup, \setminus, \{, \}, \text{or } \neg . (Thus, you must write out the definitions of some set theory notation, and you must use equivalences to get rid of any occurrences of \neg .)

  1. \mathcal F \subseteq \mathcal P (A)
  2. A \subseteq \{2n + 1 \mid n \in \mathbb{N}\}
  3. \{n^2 + n + 1 \mid n \in \mathbb{N} \} \subseteq \{2n + 1 \mid n \in \mathbb{N} \}
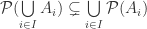
  4. \mathcal P (\bigcup \limits _{i \in I} A_i) \subsetneq \bigcup \limits _{i \in I} \mathcal P (A_i)

 

Solution

1.

\mathcal F \subseteq \mathcal P (A)

\mathcal F is a family of sets. Any member of \mathcal F , a set, is a power set of A.

So 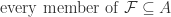\text{every member of } \mathcal F \subseteq A .

Every member of \mathcal F is in $latex  \mathcal P(A) $

\forall y (y \in F \to y \in \mathcal P(A))

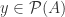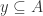To say that y \in \mathcal P (A) means that y \subseteq A .

\forall y (y \in F \to y \subseteq A)

We’ll introduce x to mean a member of y.

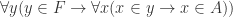
\forall y (y \in F \to \forall x ( x \in y \to x \in A))

2.

A \subseteq \{2n + 1 \mid n \in \mathbb{N}\}

Definition of subset:

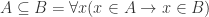
A \subseteq B = \forall x (x \in A \to x \in B)

\forall x ( x \in A \to \exists n \mathbb{N} (x = 2n + 1))

3.

\{n^2 + n + 1 \mid n \in \mathbb{N} \} \subseteq \{2n + 1 \mid n \in \mathbb{N} \}

Definition of subset:

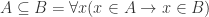
A \subseteq B = \forall x (x \in A \to x \in B)
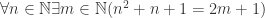
\forall n \in \mathbb{N} \exists m \in \mathbb{N} (n^2 + n + 1 = 2m + 1)

Need to use n and m to allow for different values, since these were two different statements.

4.

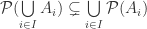
\mathcal P (\bigcup \limits _{i \in I} A_i) \subsetneq \bigcup \limits _{i \in I} \mathcal P (A_i)

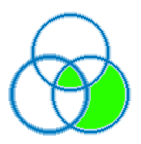
There is some set that is a power set of the union of the family of A that is not a subset of the union of all power sets of the family of A.

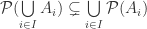
\mathcal P (\bigcup \limits _{i \in I} A_i) \subsetneq \bigcup \limits _{i \in I} \mathcal P (A_i)

Add some context

\exists y [ y \in \mathcal{P} (\bigcup \limits_{i \in I} A_i) \land y \notin \bigcup \limits_{i \in I} \mathcal P(A_i)]

Power Set: 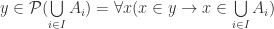y \in \mathcal{P} (\bigcup \limits_{i \in I} A_i) = \forall x (x \in y \to x \in \bigcup \limits_{i \in I} A_i) .

\exists y [ \forall x (x \in y \to x \in \bigcup \limits_{i \in I} A_i) \land y \notin \bigcup \limits_{i \in I} \mathcal{P}(A_i)]

Family Union: x \in \bigcup \limits_{i \in I} A_i = \exists i \in I (x \in A_i)

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land y \notin \bigcup \limits_{i \in I} \mathcal{P}(A_i)]

Negation

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land \neg (y \in \bigcup \limits_{i \in I} \mathcal P(A_i))]

Does this work? What does it mean to be a union of power sets? Same goes for the question itself.

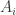Family Union: y \in \bigcup \limits_{i \in I} \mathcal P(A_i) = \exists i \in I \forall x (x \in y \to x \in \mathcal P(A_i) . If y contains all the members x, then there is a set A_i that also contains all members x.

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land \neg (\exists i \in I \forall x (x \in y \to x \in \mathcal P(A_i)))]

Power Set: x \in \mathcal P(A_i) = x \in y \to x \in A_i

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land \neg (\exists i \in I \forall x (x \in y \to (x \in y \to x \in A_i)))]

Conditional

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land \neg (\exists i \in I \forall x (x \notin y \lor x \notin y \lor x \in A_i)))]

Tautology

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land \neg (\exists i \in I \forall x (x \notin y \lor x \in A_i)))]

Quantifier Negation and DeMorgan

\exists y [ \forall x (x \in y \to \exists i \in I (x \in A_i)) \land (\forall i \in I \exists x (x \in y \land x \notin A_i)))]

How To Prove It by Velleman

Prove It by Velleman, Section 2.2, Problem 2

Leave a comment

Problem

Negate these statements and then reexpress the results as equivalent positive statements. (See Example 2.2.1)

  1. There is someone in the freshman class who doesn’t have a roommate.
  2. Everyone likes someone, but no one likes everyone.
  3. \forall a \in A \exists b \in B (a \in C \iff b \in C)
  4. \forall y > 0 \exists x (ax^2 + bx + c = y)

 

Solution

1.

There is someone in the freshman class who doesn’t have a roommate.

Let F(x) = x is a freshman

Let R(x) = x has a roommate

\exists x [F(x) \land \neg R(x)]

Negate

\neg \exists x [F(x) \land \neg R(x)]

Quantifier Negate

\forall x \neg [F(x) \land \neg R(x)]

DeMorgan

\forall x [\neg F(x) \lor R(x)]

Conditional

\forall x [F(x) \to R(x)]

If you’re a freshman, you have a roommate.

2.

Everyone likes someone, but no one likes everyone.

Let L(x,y) = x likes y

\forall x \exists y L(x,y) \land \neg \exists x \forall y L(x,y)

Negate

\neg [ \forall x \exists y L(x,y) \land \neg \exists x \forall y L(x,y) ]

DeMorgan

\neg \forall x \exists y L(x,y) \lor \exists x \forall y L(x,y) ]

Quantifier Negate, Twice

\exists x \forall y \neg L(x,y) \lor \exists x \forall y L(x,y)

There is someone that dislikes everyone, or there is someone that likes everyone.

 

3.

\forall a \in A \exists b \in B (a \in C \iff b \in C)

Negate

\neg \forall a \in A \exists b \in B (a \in C \iff b \in C)

Quantifer Negate, Twice

\exists a \in A \forall b \in B \neg (a \in C \iff b \in C)

Biconditional

\exists a \in A \forall b \in B \neg [(a \in C \to b \in C) \land (b \in C \to a \in C)]

DeMorgan

\exists a \in A \forall b \in B [\neg (a \in C \to b \in C) \lor \neg (b \in C \to a \in C)]

Conditional

\exists a \in A \forall b \in B [\neg (a \notin C \lor b \in C) \lor \neg (b \notin C \lor a \in C)]

DeMorgan

\exists a \in A \forall b \in B [(a \in C \land b \notin C) \lor (b \in C \land a \notin C)]

4.

\forall y > 0 \exists x (ax^2 + bx + c = y)

Negate

\neg \forall y > 0 \exists x (ax^2 + bx + c = y)

Quantifier Negate, Twice

\exists y > 0 \forall x \neg (ax^2 + bx + c = y)

\exists y > 0 \forall x (ax^2 + bx + c \neq y)

How To Prove It by Velleman

Prove It by Velleman, Section 2.2, Problem 1

1 Comment

Problem

Negate these statements and then reexpress the results as a equivalent positive statement. (See Example 2.2.1)

  1. Everyone who is majoring in math has a friend who needs help with his homework.
  2. Everyone has a roommate who dislikes everyone.
  3. A \cup B \subseteq C \setminus D
  4. \exists x \forall y [y > x \to \exists z (z^2 + 5z = y)]

 

 

Solution

1.

Everyone who is majoring in math has a friend who needs help with his homework.

Let M(x) = x majors in math

Let F(x and y) = x and y are friends

Let H(x) = x needs help

Answer Key says \exists [M(x) \land \forall y ( F(x,y) \to \neg H(y))] . I don’t see why it should be an implication.

\forall x (M(x) \to \forall y [F(x,y) \land H(y)])
Negate

\neg \forall x (M(x) \to \forall y [F(x,y) \land H(y)])

Quantifier Negate

\exists x \neg (M(x) \to \forall y [F(x,y) \land H(y)])

Conditional

\exists x \neg ( \neg M(x) \lor \forall y [F(x,y) \land H(y)])

DeMorgan

\exists x ( M(x) \land \neg \forall y [F(x,y) \land H(y)])

Quantifier Negation

\exists x ( M(x) \land \exists y \neg [F(x,y) \land H(y)])

DeMorgan

\exists x ( M(x) \land \exists y [\neg F(x,y) \lor \neg H(y)])

There exists a math major and that math major has no friends at all or has friends that don’t need help.

 

2.

Everyone has a roommate who dislikes everyone.

Let R(x, y) = x has a roommate y

Let L(x, y) = x likes y

\forall x \exists y[R(x,y) \land \forall z \neg L(y,z)]

Negate

\neg \forall x \exists y[R(x,y) \land \forall z \neg L(y,z)]

Quantifier Negate

\exists x \neg \exists y[R(x,y) \land \forall z \neg L(y,z)]

Quantifier Negate

\exists x \forall y \neg [R(x,y) \land \forall z \neg L(y,z)]

DeMorgan

\exists x \forall y [\neg R(x,y) \lor \neg \forall z \neg L(y,z)]

Quantifier Negate

\exists x \forall y [\neg R(x,y) \lor \exists z L(y,z)]

Someone does not have any roommates or has a roommate that likes at least one person.

3.

A \cup B \subseteq C \setminus D

\forall x [(x \in A \lor x \in B) \to (x \in C \land x \notin D)]

Negate

\neg \forall x [(x \in A \lor x \in B) \to (x \in C \land x \notin D)]

Conditional

\neg \forall x [\neg (x \in A \lor x \in B) \lor (x \in C \land x \notin D)]

Quantifier Negation

\exists x \neg [\neg (x \in A \lor x \in B) \lor (x \in C \land x \notin D)]

DeMorgan

\exists x [(x \in A \lor x \in B) \land \neg (x \in C \land x \notin D)]

DeMorgan

\exists x [(x \in A \lor x \in B) \land (x \notin C \land x \in D)]

Associative

\exists x [(x \in A \lor x \in B) \land x \notin C \land x \in D]

 

4.

\exists x \forall y [y > x \to \exists z (z^2 + 5z = y)]

Negate

\neg \exists x \forall y [y > x \to \exists z (z^2 + 5z = y)]

Quantifier Negate

\forall x \neg \forall y [y > x \to \exists z (z^2 + 5z = y)]

Quantifier Negate

\forall x \exists y \neg [y > x \to \exists z (z^2 + 5z = y)]

Conditional

\forall x \exists y \neg [\neg (y > x) \lor \exists z (z^2 + 5z = y)]

DeMorgan

\forall x \exists y [(y > x) \land \neg \exists z (z^2 + 5z = y)]

Quantifier Negate

\forall x \exists y [(y > x) \land \forall z \neg (z^2 + 5z = y)]

\forall x \exists y [(y > x) \land \forall z (z^2 + 5z \neq y)]